{{error}}
{{error}}

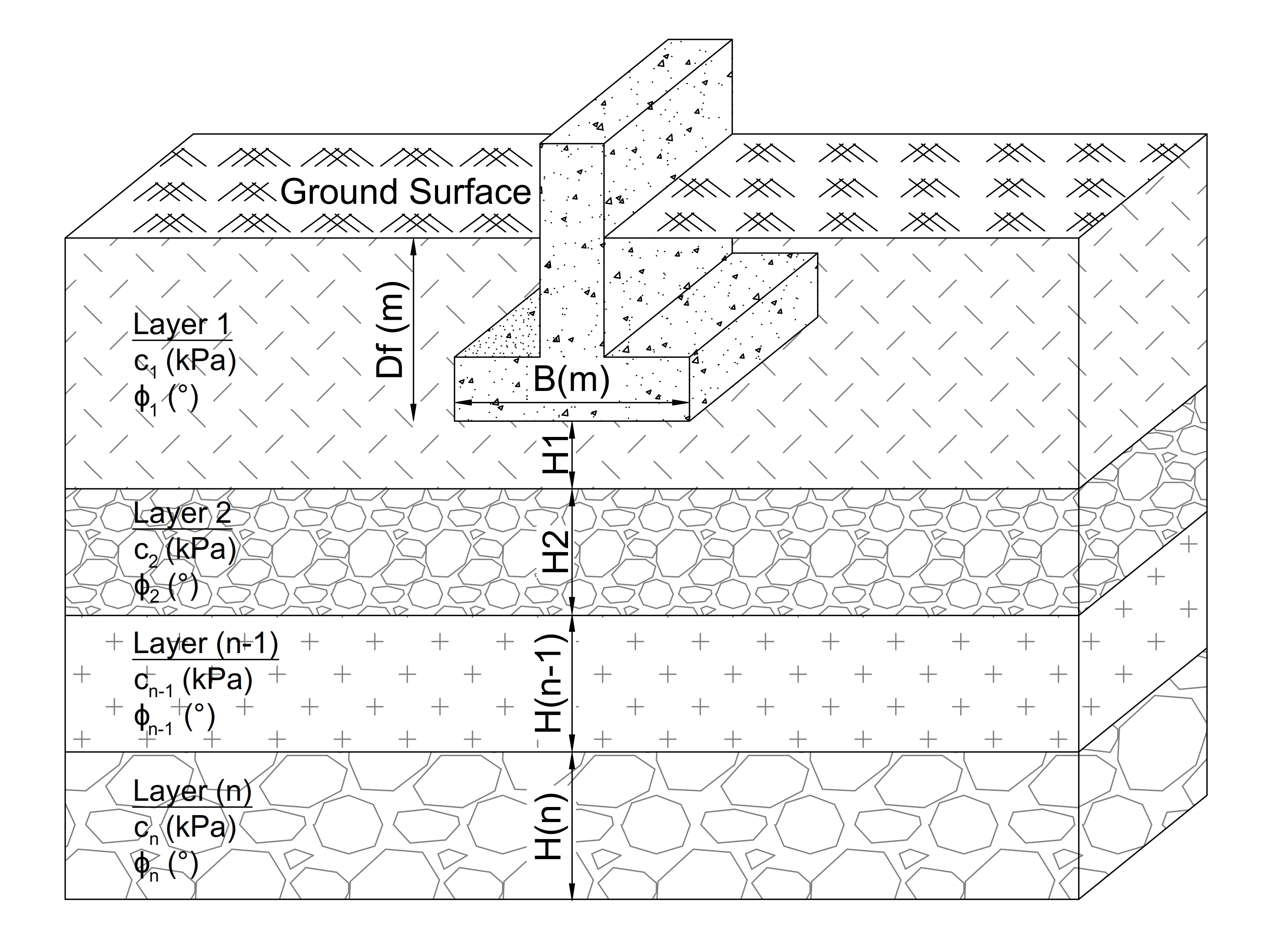
The calculation tool given above for calculating average c-φ for layered soils follows the procedure given in "Foundation Analysis and Design, 5th Edition (Joseph E. Bowles) - Chapter 4. The details, formulations and procedure of the calculations are given below.
The average cohesion and internal friction angle of the soil profile is calculated as follows:
$$c_{av} = {c_1H_1 + c_2H_2 + c_3H_3 + ...+c_nH_n \over \sum H_i} $$
$$\phi_{av} = tan^{-1}\left({H_1tan\phi_1 + H_2tan\phi_2 + H_3tan\phi_3 + ...+H_ntan\phi_n \over \sum H_i}\right) $$
Where;
cav: Average cohesion of entire soil profile
φav: Average friction angle of entire soil profile
ci: Cohesion of single soil layer
φi: Friction angle of single soil layer
Hi: Thickness of single soil layer
The effective shear depth is approxiamtely:
$$H_e = 0.5Btan(45+\phi/2) $$
Where;
B: Foundation width
φ: Friction angle of the soil layer under the foundation
Firstly, He is calculated using the friction angle of the soil layer just under the foundation to determine the contributing soil layers. After that, using the formulations given above and the c-φ values of the soil layers inside the effective shear zone(He), first set of cav and φav vaules are calculated (Iteration-0).
Secondly, another He is calculated using the φav value calculated in iteration-0. Using the new He, a new set of cav and φav are calculated (Iteration-1).
This procedure continues until the difference between the new He and previous He is less than 0.0001.The cav and φav values calculated in the last iteration are the final results. These values can be used in a bearing capacity calculation of a shallow foundation sitting on a layered soil. Bearing capacity of a shallow foundation can be calculated using Terzaghi(1943) and Meyerhof(1963) methods.